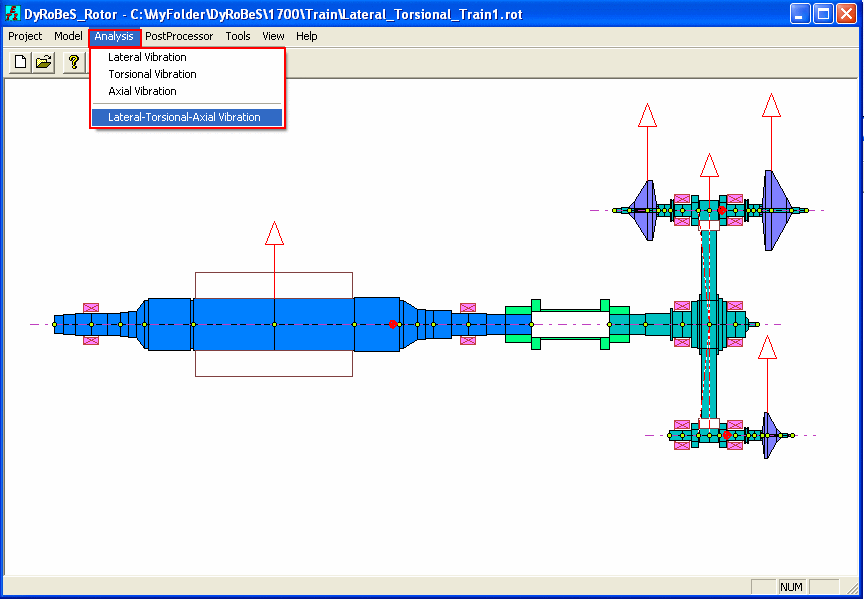
Coupled Lateral-Torsional-Axial Vibration Analysis

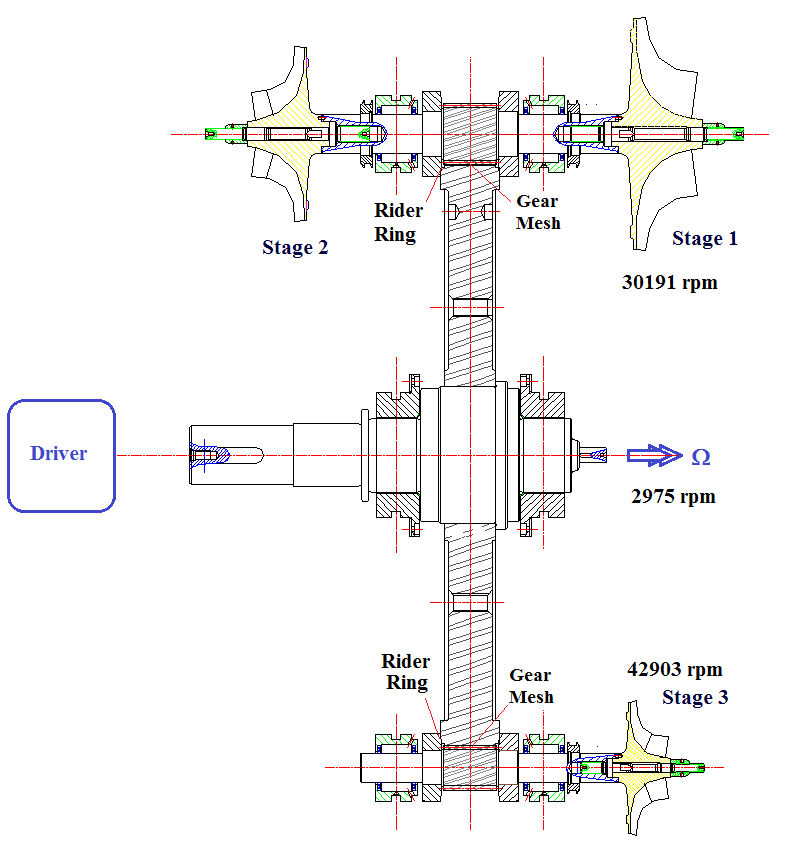
Coupled Lateral-Torsional-Axial Vibration Analysis

For a geared system, the lateral, torsional, and axial motions are coupled though the gear mesh and/or rider ring (thrust collar).

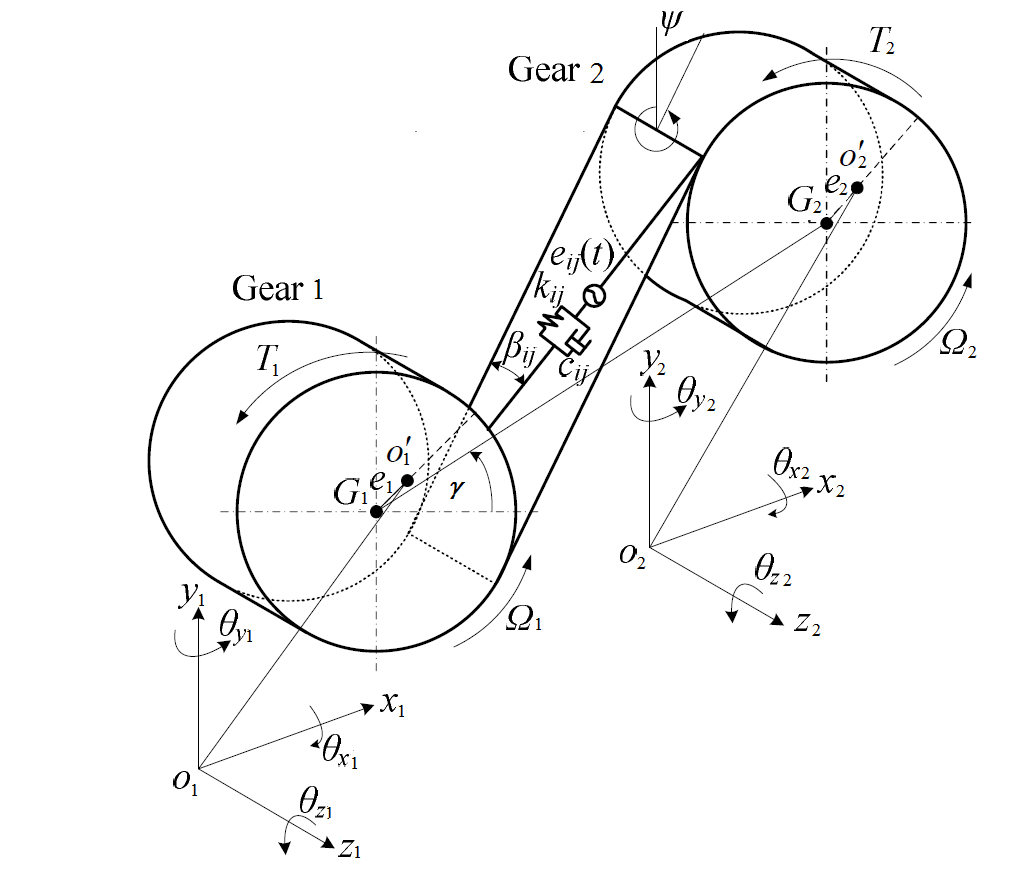
To be consistent with the coordinate system, the generalized displacements at each station contain 3 translational (x,y,z) and 3 rotational (θx, θy, θz ) displacements., as shown below:

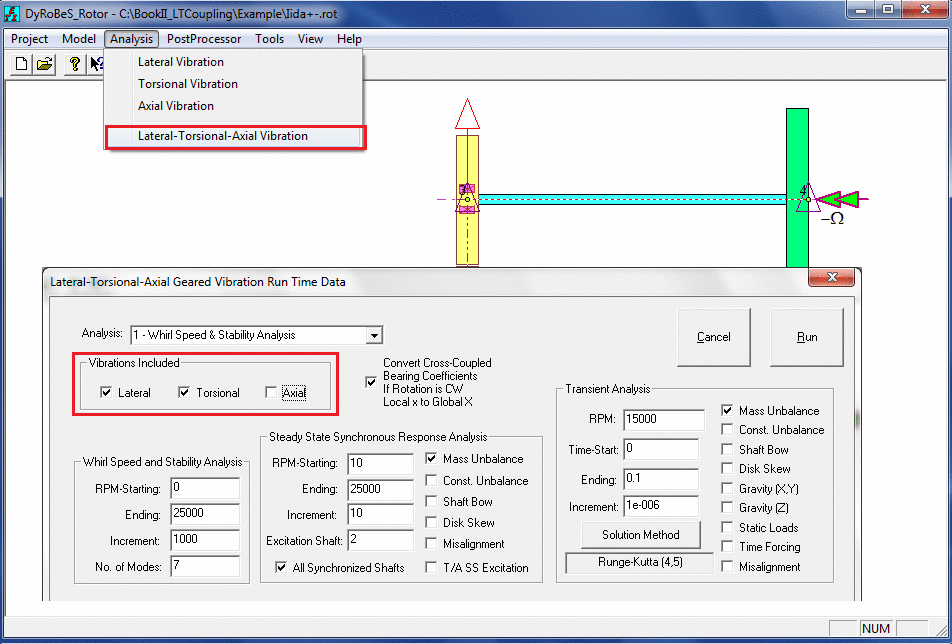
Note that in this coupled lateral-torsional-axial vibration analysis, one has the option to include all 3 vibrations, or just one vibration, or any combinations.

When analyzing the geared rotor systems and the motion at each finite element station is defined in above figure, then the following cautions must be taken:

Treat the rotor rotational speed ? as a vector, positive if it rotates in the positive Z direction (CCW for a right hand ruled Cartesian coordinate system) and negative if it rotates in the negative Z direction (CW). This will take care of the gyroscopic matrix and related forcing function involved rotational speed.

Change the cross-coupled bearing stiffness and damping coefficients if necessary when the rotor speed is negative, since almost all the bearing coefficients are obtained by assuming the rotor speed is positive in the positive Z direction. This is particularly important when performing the stability analysis since cross-coupled stiffness coefficients, including the aerodynamic cross-coupling term, significantly affect the system stability.

When viewing the results for lateral motion, the direction of whirling needs to take into account the rotor speed. That is, the forward or backward whirl is defined by the product of and , not just as used for a single rotor system.

For more details on this coupled lateral-torsional-axial vibration, please reference the document.