
Squeeze film dampers can be modeled with or without centering springs. The centering spring is assumed to be isotropic if exists. For the nonlinear centering spring, a generalized non-linear isotropic bearing can be used in parallel or in series with the squeeze film damper. In the steady state synchronous response analysis, centered circular orbits are assumed. The general motion of a plain fluid film journal bearing or a squeeze film damper is governed by the Reynolds equation, which is derived from the Navier-Stokes equation. The fluid film forces acting on the journal are determined by application of boundary conditions and integration of pressure distribution. The general incompressible laminar Reynolds equation is given by:

For a squeeze film damper, the damper is free to precess, but not rotate. Furthermore, the last term vanishes at steady state condition. For the transient analysis, short bearing and pi film assumptions are utilized. For the steady state response, the following table summarizes the equivalent stiffness and damping for the cases of circular synchronous motion about the origin and pure radial motion with no precession for the conditions of cavitation (pi film) and no cavitation (2pi film).
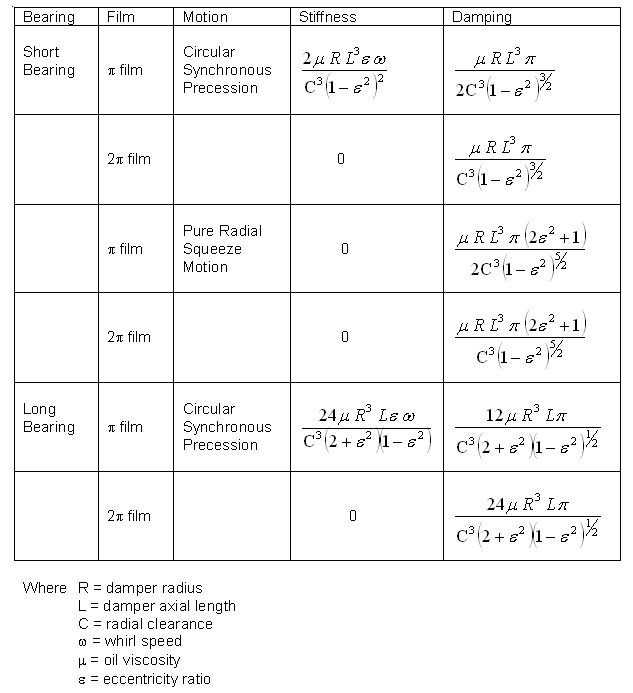
Note that for the circular synchronous motion, the equivalent stiffness term is a highly nonlinear function of eccentricity and may lead to a nonlinear jump phenomenon under high rotor unbalance. Caution must be taken while designing the damper, since it can significantly either improve or degrade the dynamic characteristics of the rotor system.
The data fields are self-explanatory. In the right bottom of the screen, the proper units for the specified unit system are displayed for reference.
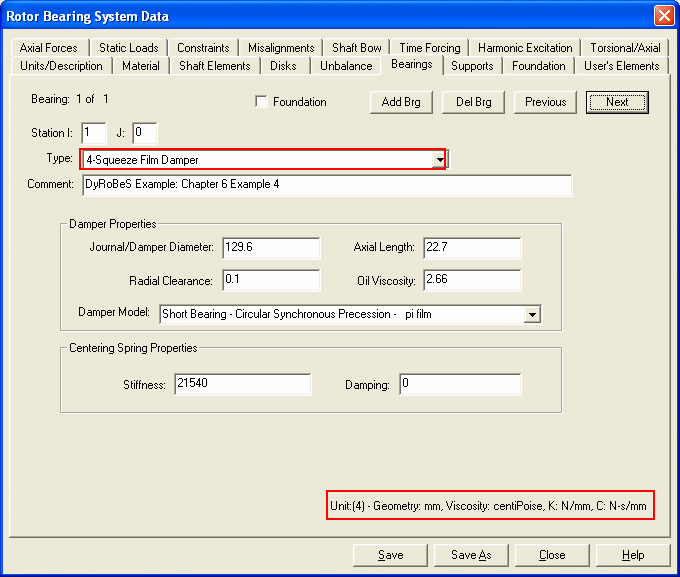
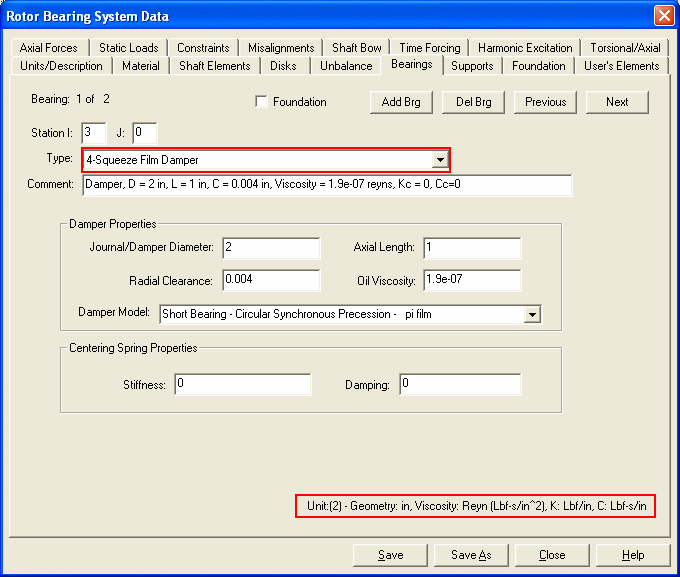
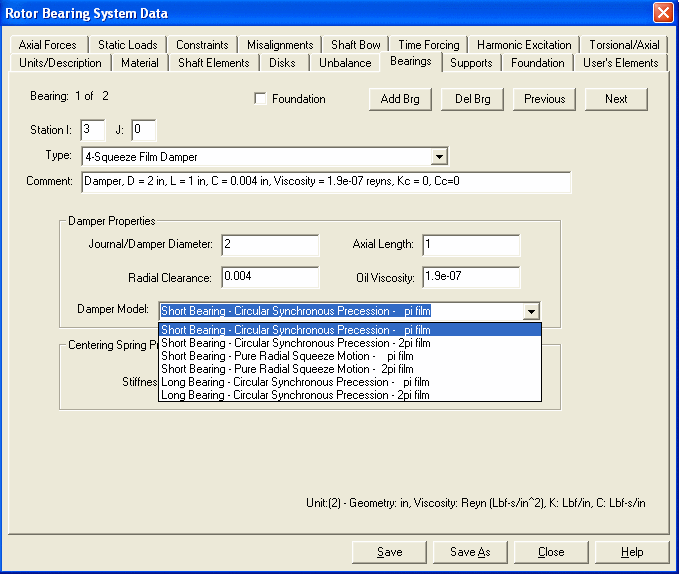
See also Bearings.
Copyright © 2014-2017